Electronic Energy Model

The Q-K procedure for recombination and the rate equation that is based on this procedure involve the ternary collision volume that is based on the equilibrium constant.  It was found that this volume is sensitive to the inclusion or omission of the electronic partition functions.  In the case of oxygen, there was a factor of fifty difference and it is the rate that includes the electronic functions that agrees with the rate in the 1966 “consensus” database of Bortner.  However, this may just be because that rate was based on measured dissociation rates and an equilibrium constant that also included the electronic partition functions.  There appears to be little data on the cross-sections for the thermal excitation of the higher electronic levels at temperatures of the order of 10,000 K.  This makes it difficult to determine whether the almost universal neglect of electronic excitation in existing DSMC and continuum CFD re-entry flow studies has led to any significant error.

Fig. 1  Equilibrium electronic energy in             high temperature air.

Fig. 2  Temperature relaxation in non-               reacting oxygen.

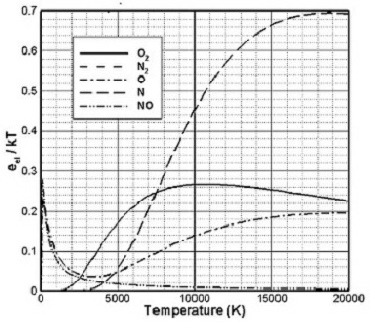
    Figure 1 is based on the electronic partition functions and shows that the average equilibrium electronic energy of the gas in the shock layer of a typical re-entry flow would be about 0.2kT.  Electronic energy therefore has the potential to have a noticeable influence on these flows.

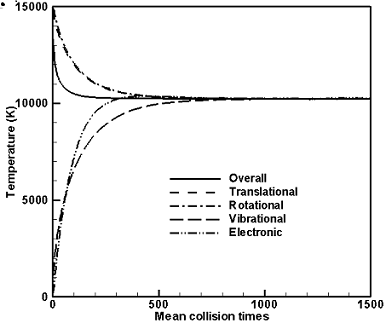
The equations for the extension of the generalized Larsen-Borgnakke to the electronic mode were written down in my 1994 book, but they were not implemented at that time.  They have now been implemented in a version of the DS1V program.  Figure 2 shows the temperature relaxation in artificially non-reacting oxygen that initially has translational and rotational temperatures of 15,000 K and vibrational and electronic temperatures of zero.  The electronic relaxation collision number has been assumed to be 100.  If the necessary data can be found, a separate collision number will be assigned to each electronic level.  The collision number is the ratio of the elastic cross-section to the cross-section for thermal electronic excitation.  The electronic temperature has been defined as the overall temperature multiplied by the ratio of the electronic energy to the equilibrium electronic energy at that temperature.  Because the equilibrium energy is a function of temperature, the overall temperature must be determined by an iterative process.  Figure 2 shows that all the temperatures come to equilibrium so that equipartition is achieved by the model.  Note that there is no ionization and Fig. 2 shows the electronic rather than the electron temperature.